题目地址：interger-repleacement

题目介绍

Given a positive integer n and you can do operations as follow:

  1. If n is even, replace n with n/2.
  2. If n is odd, you can replace n with either n + 1 or n - 1.
    What is the minimum number of replacements needed for n to become 1?

Example 1:

1
2
3
4
5
6
Input:
8
Output:
3
Explanation:
8 -> 4 -> 2 -> 1

Example 2:

1
2
3
4
5
6
7
8
Input:
7
Output:
4
Explanation:
7 -> 8 -> 4 -> 2 -> 1
or
7 -> 6 -> 3 -> 2 -> 1

算法分析

面对每个数字有两种情况:

  1. 当n为偶数时将n变为n/2
  2. 当n为奇数时又面临两种选择一种是将n变为n-1,另一种是将n变为n+1,这两种都会将n变为偶数，此时又回到第一种情况，很容易推出最终都会把n变为1。题目要求我们寻找最少的变化替换，在n为奇数时有两种选择，很容易想到可以使用递归的方法。

递归解

递归形式解：
1
2
3
4
5
6
7
8
9
10
int integerReplacement(int n) {
    if(n == INT_MAX)
        return 32;
    if(n==1)
        return 0;
    if(n%2==0)
        return 1 + integerReplacement(n/2);
    else
        return 1 + min(integerReplacement(n-1),integerReplacement(n+1));
    }

这种方法很直接，代码易读简洁，下面看一个在leetcode上运行时间排在最前面（目前为止）的解法:

直接求解

直接求解：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int integerReplacement(int n) {
       int ans = 0;
       size_t m = n;
       //见下面解释一
       auto tailingZeros = [](size_t m) {
           int cnt = 0;
           while(0 == (m & 1)) m >>= 1, ++cnt;
           return cnt;
       };
       while(1 != m) {
           if(1 == (m & 1)) {
           	 //见下面解释三
               if (0 == ((m - 1) & (m - 2))) --m;
               //见下面解释二
               else m = tailingZeros(m - 1) >= tailingZeros(m + 1) ? m - 1: m + 1;
           }
           else m >>= 1;
           ++ans;
       }
       return ans;
   }

解释一:

1
2
3
4
5
6
auto tailingZeros = [](size_t m) {
            int cnt = 0;
            while(0 == (m & 1)) m >>= 1, ++cnt;
            return cnt;
        };
这里使用了Lmbbda表达式，tailingZeros方法是用来计算末尾零的个数

解释二:
　　当m为奇数时，判断m+1和m-1末尾零的个数，选择末尾零个数大的那个值作为替代值。因为除以2的操作，对于整数型（int）的数字来说在二进制中就是左移操作，那么末尾零的个数越多的意味着可以移动更多位，那么所需要的操作就会达到最少。

解释三:

1
if (0 == ((m - 1) & (m - 2))) --m;

因为此时m为奇数，那么m-1为偶数，m-2还是为奇数。我们可以令
$$
t=m-1，则 t-1 = m-2
$$

如果
$$
t&(t-1)=0
$$

则说明$t$ 与 $t-1$的每一位都是相反的，而又因为$t$与$t-1$只相差1，而t的末尾为0，$t-1$的末尾为1，那么满足这样的条件的t只能为所有位只有一位为1，其余全为0，假设$t$中1的位置为$x$，那么$t-1$就为最后$x-1$位全为1.其余全为0.并且这个条件时充分必要的。
证明:
(反证法)：如果$t-1$不满足上述条件，$t&(t-1)=0$.
$t-1$为奇数，末尾为1，则加1后产生进位，那么与它相邻的1会变为0，并再次产生进位，以此递推，如果$t-1$不满足上述条件，那么在非最后几位相邻的1中的值不会产生进位加1的效果，所以这个位置的1会保持不变，从而这一位与的结果不为0，与结果相悖。可以参照下面的例子。

Example:

1
2
3
4
5
6
7
8
t-1 =  0b00101111; 
t= 0b00101111+0b1 =0b00110000

t&(t-1) = 0b00110000 
        & 0b00101111 
        -------------
        = 0b00100000
结果并不等于0

从上面分析可以看出如果m-1满足所有位只有一位为1，其余全为0，那么可以直接一直左移直到这位1一直移动到末尾，达到最少操作。
这个if语句的最用是提前判断这种特殊情况以免进入下面的tailingZeros函数判断，起到一定优化的作用。

当然可以去除这个if，直接使用下面的else判断，也是可以的。但是这里需要排除一个特殊情况就是3(0b11),之所以特殊因为3+1= 0b100 的末尾有两个0，而3-1 = 0b10 末尾有一个零如果按照推断则需要选择3+1，但是此时选择3-1所需的步数才是最小的。

所以这段代码非优化为（仅列出m为奇数的代码片段）:

1
2
3
4
if(1 == (m & 1)) {
    if (3==m) --m;
    else m = tailingZeros(m - 1) >= tailingZeros(m + 1) ? m - 1: m + 1;
}

至此这段代码分析完毕。

简单版本

这个版本是我在分析leetcode代码最快运行时间也就是第二种算法想到的，应该是目前为止比较简单的版本吧：

1
2
3
4
5
6
7
8
9
10
11
12
int ans = 0;
    size_t m = n;
    while (1 != m) {
        if (1 == (m & 1)) {
            if (m == 3) --m; //special case
            //见下面分析
            else m = (m & 0b11 ^ 0b01) ? m + 1 : m - 1;
        }
        else m >>= 1;
        ++ans;
    }
    return ans;

分析
在这个版本中我去除了第二种版本判断末尾零的个数的判断方法。
因为m为奇数，最后两位仅有两种情况11和01两种，所以我从这两种情况出发来判断。

  1. 首先看末尾为11这个情况:
    当一个末尾数为11时当加1过后末尾至少有两个零，而减一仅为一个0，按照第二种算法选择末尾零个数最多的数，此时应该选择m+1。
  2. 同理看末尾为01这个情况:
    当这个数加1过后末尾仅一个0，减一后至少2个零，同理此时应该选择m-1。

一 为什么3是特殊情况
　　在第二种非优化和第三种算法种都排除了3这个特殊情况，为什么需要排除
设 m为末尾连续x位为1,其余全为0。如果我们采取加1，那么仅第x+1位（从最末尾开始算）为0，则需要x次左移使得结果为1.
总共需要x+1次操作。而采取减1移位，每两次操作可以移走一位1，则总共需要2（x-1）次。那么如果要使得加1操作最少的话
则$x+1 \leq 2(x-1)$ 解得$x \geq 3$ 也就是说最少需要末尾3个1，则排除掉3。

二 为什么需要删除末尾零个数多的
我们来探讨最后两位为1的情况
我们上面已经说明了如果仅末尾有连续的1，那么加1操作后就可以一直左移，（3特殊）。
那么另外一种情况就是除了末尾连续的1还存在其余位有1的情况。这种情况如下图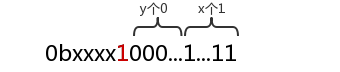

如果我们需要将红色的1移动到最后1位那么如果采取加1操作则需要x+y+1次操作。如果每次都采取减一操作则总共需要2x+y次操作。
注意这里的x是大于2的。所以(x+y+1)<(2x+y)的。
同理可以探讨末尾位01的情况。

通过分析不难得出 

1
m = (m & 0b11 ^ 0b01) ? m + 1 : m - 1;

判断m两种情况的代码。

（完）