传统的解释图神经网络是从傅里叶变换着手，本文拟从另一个角度来解释图卷积神经网络，先从一个直观的角度入手，然后使用数学的语言加以描述。

1.那么首先什么是卷积？

卷积是一种运算，可以看成两个函数（信号）互相作用的一种结果。如果是离散的点，看成向量，卷积就是一种加权和，这也是为什么CNN利用卷积来抽取特征。可以参考这篇文章：
https://www.zhihu.com/question/22298352
$$(f*g)(n)=\sum_{\tau=-\infty}^{\infty}{f(\tau)g(n-\tau)}$$

2.图卷积和CNN的卷积

图（Graph）是一种拓扑结构，与二维平面的图片（Picture）的结构（grid）不同，如果我们把图上的顶点编上号，按序排放，每一维即该顶点所代表的值，也可以组成一个二维的矩阵，那么我们是否也可以按照CNN的方式，定义一个filter在这个图上滑动来进行卷积呢？显然是不行的，因为首先图的结构并不是grid，也就是说我们的编号是随机的，编号为1的点和编号为2的点虽然在矩阵的位置是相邻，但它们可能在图上并没有连接的边，或者边的权重很小，所以利用CNN的卷积的方式，卷积的结果并不代表任何意义。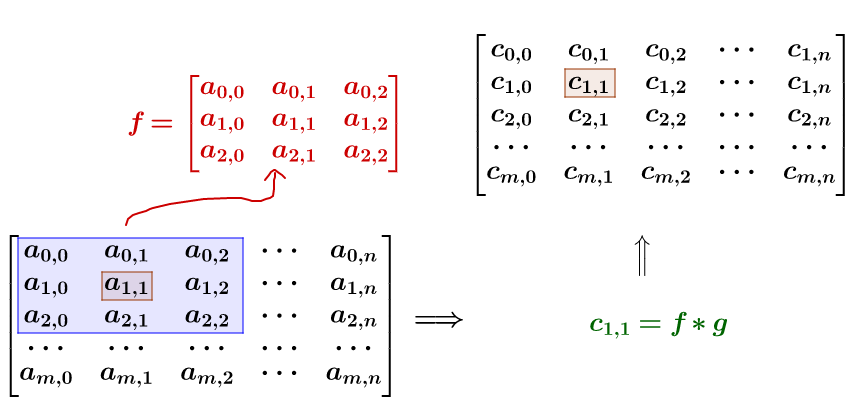

3.图的转换

既然直接在图所构成的矩阵上不能卷积，那么是否可以将图进行某种转换，然后做卷积？很多论文以及博客都从这儿开始使用傅立叶的方式来解释，我们将图进行傅立叶变换，将其化成一些基向量（基信号），然后我们在频率域做卷积，然后再将卷积后的结果进行傅立叶逆变换成时域信号。而基向量的选择则是拉普拉斯矩阵的特征向量，至于为什么，是因为其和实数的傅立叶变换的基信号都满足拉普拉斯特征方程，那么为什么要满足特征方程？似乎很多地方都没有涉及？所以我准备从另一个角度来解释。

首先回到我们最开始的问题，需要在图上做卷积操作，但是如果想要使用类似于CNN的卷积，也即在数据所代表的矩阵上不断的滑动然后内积获得结果。这么做的物理意义是因为对于图片来说，它四周的像素点的变化往往非常相关的（局部相关），通俗的说如果图片某个位置的像素点为红色，那么其四周为红色的概率是很大的，所以通过卷积我们可以得到某个像素点与其周围像素的一个加权的平滑表示，从而从图片中抽取特征。

对于图结构的数据来说，我们描述它周围的点往往是根据其邻居边（在这里我们以无向边进行说明）的权值来描述，权值越大也说明这两个点的相关性越高（可以类比于图片周围的像素）。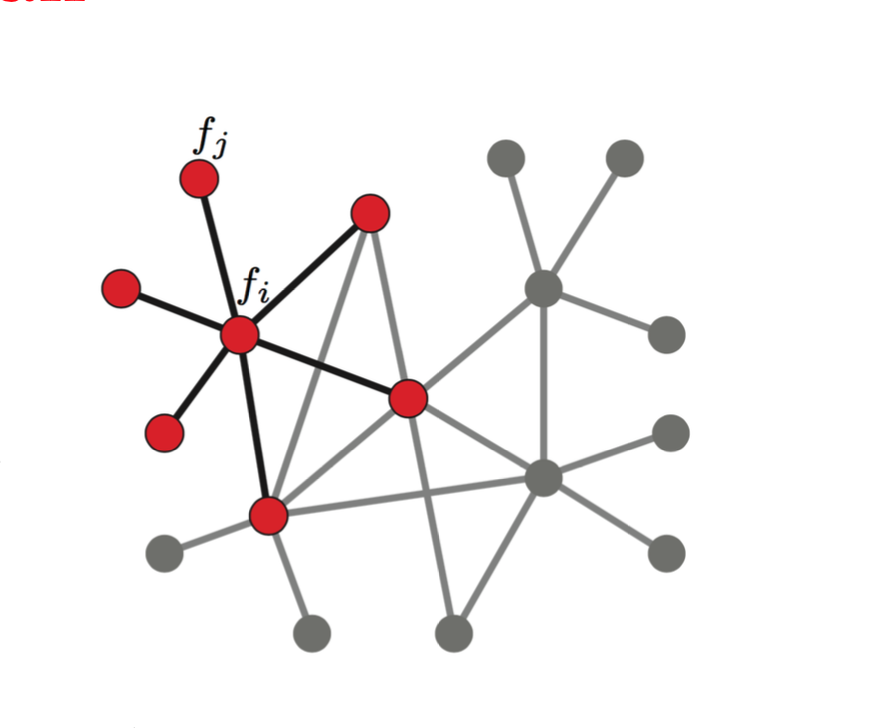
graph.png

所以我们在卷积的时候其实就可以根据这种相关性来卷积，即让相关性大的维度让他们相邻，即重拍序号，然后再做卷积。但是这么做有什么弊端？不同的点周围的相关性的点往往是不一样的，那么也即是说还是会有N（点的个数）个不同的排列方式，需要N个不同的filter，不能参数共享。而我们知道对于一个N维向量来说，我们可以找到N个基向量来任意的表达它们，如果我们将它们进行某种线性变换，变换到另一种坐标维度下，使得这些图的信号在某一个维度下是具有相关性的，那么我们就可以在新的坐标维度下进行卷积操作，然后再变换回去。

什么意思呢？图不是变成了一个向量了吗，这个向量是由很多基向量组成的，那我们如果变换基向量（线性变化），使得该图在每一个维度下的投影是非常相关的，也就是在维度下点与点都是很平滑的，一个点的变化周围的点的变化是比较一致的，比较相关的（可以看成一种局部信号的聚类）。那么此时一个图就可以变成很多个具有局部相关性的基向量（当然基向量之间是正交的），此时我们对基向量进行卷积操作，然后将卷积之后的结果再通过逆变换回去就可以了，可以说是非常的Amazing啊。

4.如何找基向量

有了上面的分析，那么如何找到这组基向量呢？如果学习过PCA我们知道，PCA是把信号映射到越远越好，也就是说投影下来这些数据分开的越远越好，恰恰相反，我们这里是想要把信号聚拢的越近越好，所以我们找到特征值最小的基向量就行了。（我觉得从PCA出发可以推一下，这里暂且放一放，而是使用图上使用比较多的dirichlet energy，可以参考下面的链接）
https://www.zhihu.com/question/392108937/answer/1220245802
Dirichlet Energy描述了一个函数的平滑程度，如果越平滑，也说明函数的变化不是非常剧烈，而是具有某种相关性。所以推广到图上，就如上面参考文献里描述的一样，基向量也就是拉普拉斯矩阵的特征向量，特征值越小，相关性越大。这里也解释了为什么是拉普拉斯，而不是其他基向量，非常的Amazing。

5.图卷积深度学习

有了基向量之后，我们就可以对原始图向量进行线性变换，即与基向量矩阵进行矩阵乘法，卷积向量做同样的运算，然后进行卷积，最终乘以基向量矩阵的逆进行反变换。这个结果和利用傅立叶推导的结果一致。

有了图卷积方法，就可以类比CNN网络对图进行深度学习，可以参考：
https://www.zhihu.com/question/54504471/answer/332657604

当然目前还是从一种直观的语言来阐述，后面会加上一些数学的推导。