如何使得 raft 算法相继两个leader 的 term 连续
Contents
我们思考一个有趣的问题,如何让每个term都选举出一个唯一合法的leader?
在raft算法中,为了能让选举能够顺利执行,规定了每个节点只能给同个term的一个node投票,candidate如果投票失败,会将自身的term+1, 高的term的优先级会比低的term高,也就是说高term可以强制让低的term的选举作废。这种规定则是为了能够顺利的选举出leader所制定的规则。这样会有一个允许发生的现象就是可能导致某个term中没有选举出leader。
那么如何让每个term都选举出一个唯一合法的leader? 当然可以完全没有这个要求?这里只是就这个问题作出探索,不涉及其他诸如: 每个term都选举出leader的用途在哪?,会不会对raft的性能造成影响等对正确性无关的问题。
下面是设想的一种具体做法,大家可以讨论一下:
加入一个新的timeout
在raft中有多个timeout,下面是一个经典的raft角色变化示意图
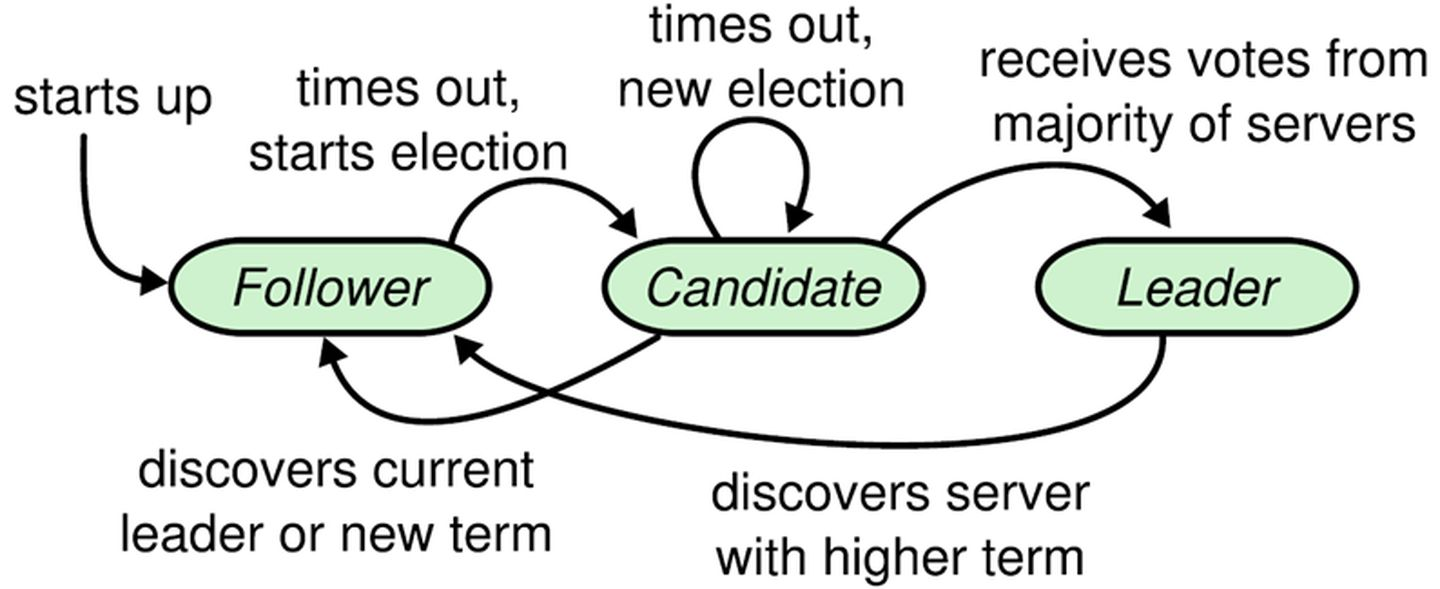
图来源于论文
新增加一个的timeout称之为 on_vote_timeout, 作用是限制投票行为的发生,也就是说当一个节点给另外的一个节点投票之后,此timeoute生效,在这个timeout时间内,不能够其他任何人投票,即使term比当前投票的人高。也可以看作是一个lease:on_vote_lease,因为其行为可能更像是lease,无论怎么命名,作用如上所述。
那么第二个问题就是这个timeout的时长设定为多少?规定 on_vote_timeout < election_timeout。 因为follower每次经过election_timeout之后,会转变为candidate,candidate会先给自身投一票,那么如果on_vote_timeout = election_timeout 那么on_vote_timeout就没有意义了,只需要一个election_timeout就可以了。那如果on_vote_timeout > election_timeout,也不行,如果是这样的话election_timeout之后,还不能给自身投票,但是却又发起了新一轮选举,会造成问题。
新的投票机制
在引入上面的on_vote_timeout之后,需要对原始的投票机制作出修改。具体规则如下:
follower转变为candinate时,先查看当前日志上一个leader的$last\_leader\_term$,并且设置新的term $new\_term = last\_leader\_term+1$, 并一直维持这个new_term作为投票的请求的term,直到这个new_term有新的leader产生(可以是自己,也可以是其他节点)。发起request_vote请求,和原始论文描述一致。- 接受到投票请求的节点,会先判断自身的
on_vote_timeout是否过期,如果过期,则可以投票。判断term的规则是当前term必须比当前节点已知的leader的term新,并且只能是$request\_term = last\_leader\_term+1$。这里值得注意的是判断的是上一个成功当选leader的term,不是和自己本身的term。
然后判断日志的规则和原始论文一致,满足上述情况,则返回true,开启on_vote_timeout,否则返回false。 - 当
candidate收到了大多数的投票,则成为on_leader,此时发送一个become_leader日志(和noop日志类似),当该日志被committed后,此节点成为leader并开始工作。这里注意的一点是,其他节点在收到日志时(append_entries请求)会判断该日志的term,以及发送者是否是自己投票的节点。
正确性证明
定理一:一个term下只会选出一个leader
首先按照上述的选举机制一个节点得到大多数投票后,如果在所有的投给自己票的节点的on_vote_timeout的最先结束的那个时间点前,将become_leader日志committed,那么一定只会有一个leader,也就是满足论文的 Election Safety: at most one leader can be elected in a giventerm.§5.2
证明:
假设一个term下有两个leader,也就是说这两个leader都将become_leader的日志复制到了大多数节点,那么这两个大多数节点集合的并集不为空集,取交集中的一个节点,也就是说它给这两个leader都投过票,并且保存了他们的become_leader日志,但是由于投票的原则,接受append_entries需要判断是否是投票节点的leader,所以必定会拒绝其中一个日志,所以假设条件不成立。证明完毕。
定理二:相继两个leader之间的term是严格连续递增的
同样可以使用反证法,假设两个相继leader之间的term是不连续的,设前一个leader的term为$m$,后一个leader的term为$n$, 即 $n > m+1$, 那么必定存在一个$k$ = $n+1$满足$n<k<m$。根据条件在term为$k$的阶段是不存在leader的,也就是带有日志的term为$k$的日志并不存在于大多数节点中。那么按照投票原则,term为$m$的leader能够被选出来,必定存在一个term为 $m-1$的leader,以此类推,必定存在一个$k = n+1$ 的leader,与假设冲突。证明完毕。
上述说明了一种如何选举出没有leader的term存在空洞的选举方法,并给出了一定的证明,可能存在一定的错误,欢迎大家讨论。