SILT 论文中关于 Entropy coding 的解释

问题引入

论文 “SILT: A Memory-Efficient, High-Performance Key-Value Store” [3] 中 Figure 5 描述了如何构建一个 trie 树（前缀树）：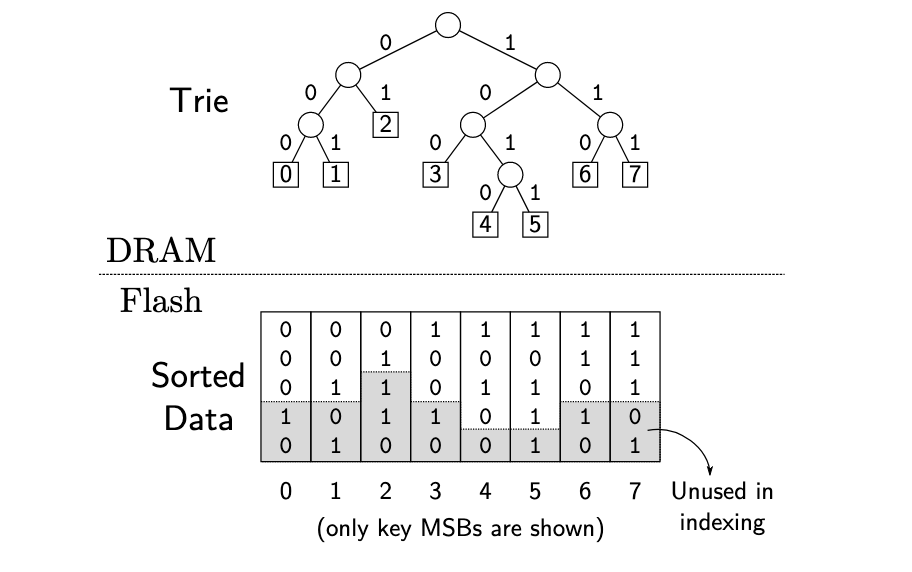
图片.png
Figure 5： Example of a trie built for indexing sorted keys. Theindex of each leaf node matches the index of the correspondingkey in the sorted keys.

trie 树中每个非叶子结点代表其后继所有结点 key 的最长公共前缀，可以提升查找速度。

在论文中的 Figure 6 (c)，提到了几种 trie 树的表示方法：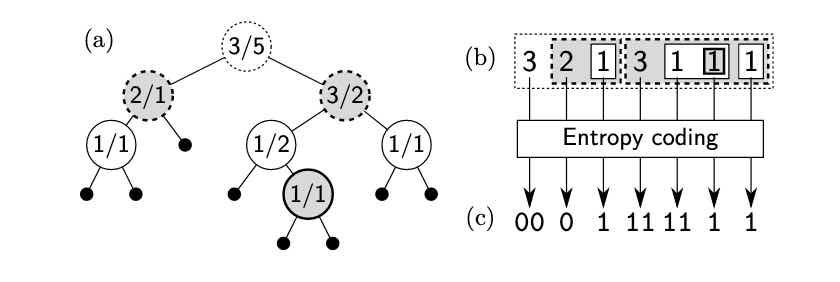
图片2.png

Figure 6: (a) Alternative view of Figure 5, where a pair of num-bers in each internal node denotes the number of leaf nodes inits left and right subtries. (b) A recursive form that representsthe trie. (c) Its entropy-coded representation used by Sorted-Store.

其中，（a）是将中间结点使用两个数字表示，第一个数字代表左子树叶子结点个数，第二个数字代表右子树的叶子结点个数；（b）是将(a)转化为数组的形式表示，在查找的时候可以根据 key 的每位上的二进制数判断，如果为0 继续到下一位，如果为 1 则跳过接下来的数字（左子树），继续判断，直到叶子结点（数字为1），从而得到其在所有数据中的offset，可以结合论文的例子理解；（c）是使用Entropy coding表示，进一步压缩空间。

关于（c）是怎么计算而来，论文没有非常明显的步骤，仅做了一些算法思想的描述

The value of|L|tends to be close to half of|T|(thenumber of leaf nodes inT) because fixed-length hashed keys are uni-formly distributed over the key space, so both subtries have the sameprobability of storing a key. More formally,$|L|∼Binomial(|T|,\frac{1}{2})$

在阅读的时候可能存在一定的疑问。针对（c）的计算方式，作如下的详细说明，欢迎指正。
（c）的作用主要是为了压缩上面的数组中的数字，因为每个数字可能出现的概率不一样，如果使用统一长度的大小来表示这些数字，一定会造成空间浪费。还好哈夫曼树[2] 可以很好的解决这个问题，哈夫曼树是根据不同的 key 的权重来构造编码方式，权重越高的所需要的编码位数越少，通常权重选择为其 key 出现的概率，所以也是一种 entropy coding。

如Figure 6(c)，在根结点中，其后继的叶子结点数$n$ 为 8，那么它左子树的大小$|L|∼Binomial(8,\frac{1}{2})$，此时的二项分布的分布列为：
图片3.png

以此为权重构建哈夫曼树，那么实际的左子树大小为$3$ ，编码即 $00$。可以使用在线哈夫曼计算器查看上述哈夫曼树。

同理数组中第二位的为 2 ，代表在（2，1）为根结点的左子树大小为 2，因为（2，1）节点是（3，5）节点的左子树的根节点，那么（2，1）这个位置的左子树的大小$|L|∼Binomial(3,\frac{1}{2})$，同理构建哈夫曼树后，因为实际左子树为2，即编码为 $0$。这里需要注意的是，在计算第二层的｜L｜的编码的时候 n 需要跟着改变（递归），类似于条件概率。这里也是理解上存在问题的关键地方。所以完成剩余结点编码后就和图中的结果是一致的。

结果验证

参考 SILT 的论文代码 https://github.com/silt/silt，其中关于此编码方式的代码位于 huffman.hpp 中, 编写测试代码：

void encode(int n,int left){
    huffman_tree_generator<uint64_t> gen(n+1);

    uint64_t v = 1;
    gen[0] = v;
    for (unsigned int k = 1; k <= n; k++)
        gen[k] = v = v * (n - k + 1) / k;

    huffman_tree<RefType> t(n + 1);
    gen.generate(t);

    auto huff = new huffman<RefType>(t);
    bit_vector<> bits;
    // encode
    huff->encode(bits,left);  
    // print
    for(size_t i =0 ;i<bits.size();i++){
        std::cout<<bits[i];
    }
    std::cout<<" ";
}


int main()
{
   // dfs encode
    encode(8,3);
    encode(3,2);
    encode(1,1);
    encode(5,3);
    encode(3,1);
    encode(1,1);
    encode(1,1);
}

输出：

1	00 0 1 11 11 1 1

与论文结果一致。

参考文献：

[1]《二項式分布》, 维基百科，自由的百科全书. 1月 31, 2021. 见于: 6月 13, 2021. [在线]. 载于: https://zh.wikipedia.org/w/index.php?title=%E4%BA%8C%E9%A0%85%E5%BC%8F%E5%88%86%E5%B8%83&oldid=64032330
[2]《Huffman coding》, Wikipedia. 5月 31, 2021. 见于: 6月 13, 2021. [在线]. 载于: https://en.wikipedia.org/w/index.php?title=Huffman_coding&oldid=1026111001
[3] H. Lim, B. Fan, D. G. Andersen和M. Kaminsky, 《SILT: A Memory-Efficient, High-Performance Key-Value Store》, 页 13.

Contents

问题引入

结果验证

参考文献：